Filtre Gaussien

Utilisé pour faire du lissage d’images, comment fonctionne le filtre gaussien?

Introduction

Le filtre gaussien est utilisé pour faire du lissage.

L’idée est de supprimer les détails en homogénéisant le rendu de l’image.

Cela a pour effet de rendre l’image de sortie plus floue que l’originale.

Dans cet article, on n’applique des filtres gaussiens uniquement à des images en niveaux de gris. En effet, l’application d’un tel filtre sur une image couleur tend à la rendre grise. On peut donc se contenter d’étudier les effets du filtre gaussien dans le cas où l’image de départ est déjà grise.

Idée

Regardons comment le filtre gaussien fonctionne.

Imaginons que l’on dispose d’une image de 25 pixels (ça ne fait pas beaucoup mais c’est pour l’exemple!), comme celle ci-dessous:

Image de départ, 5×5

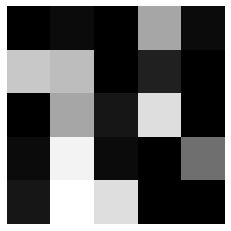
On voit qu’il y a des pixels noirs à côté de pixels beaucoup plus clairs.

Mais on aimerait que la transition entre les pixels clairs et les pixels foncés soit plus douce.

En d’autres termes, on veut lisser l’image.

Une possibilité est d’appliquer un filtre gaussien.

Commençons par traduire notre image de 25 pixels en des valeurs numériques qui représentent les nuances de gris:

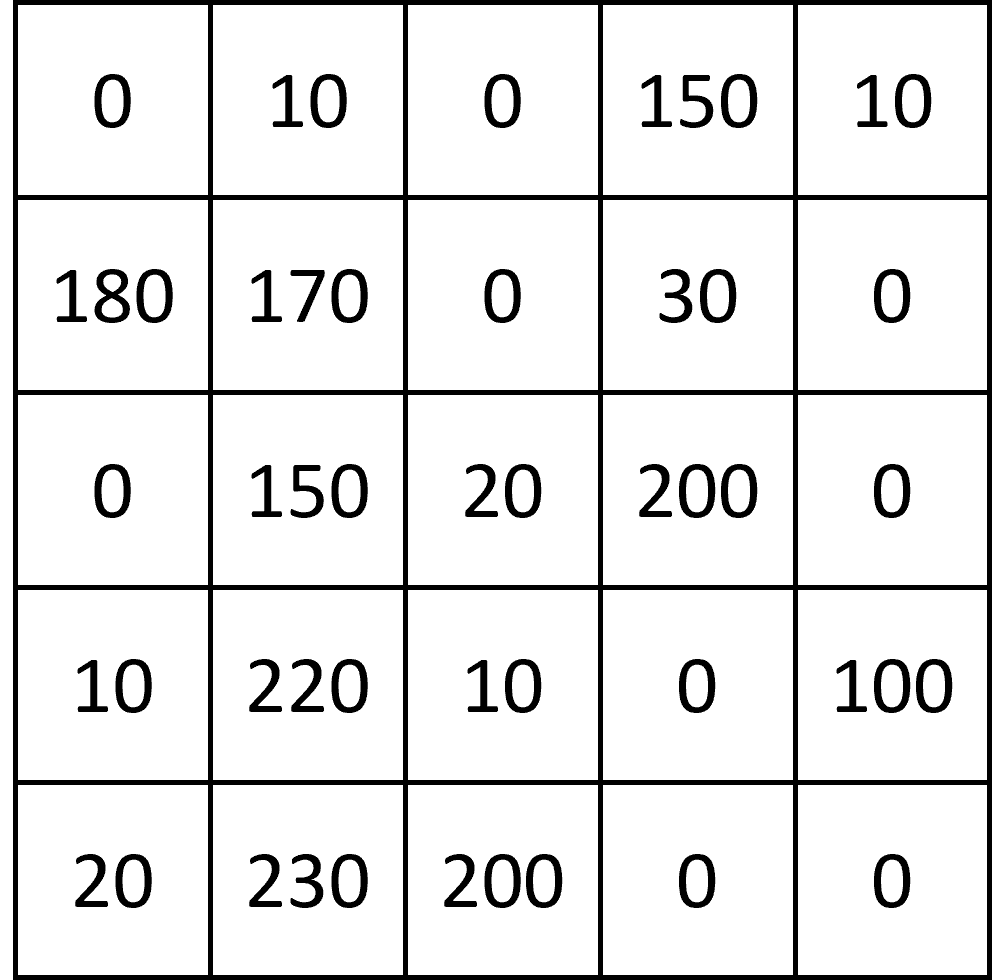
Image traduite en valeurs numériques

Pour simplifier la lecture, j’ai choisi des valeurs rondes (qui finissent par un 0). Ce sont des valeurs entre 0 et 255 qui représentent les nuances de gris, avec 0 correspondant à du noir et 255 à du blanc.

Munissons à présent cette grille de deux axes:

Valeurs numériques avec des axes

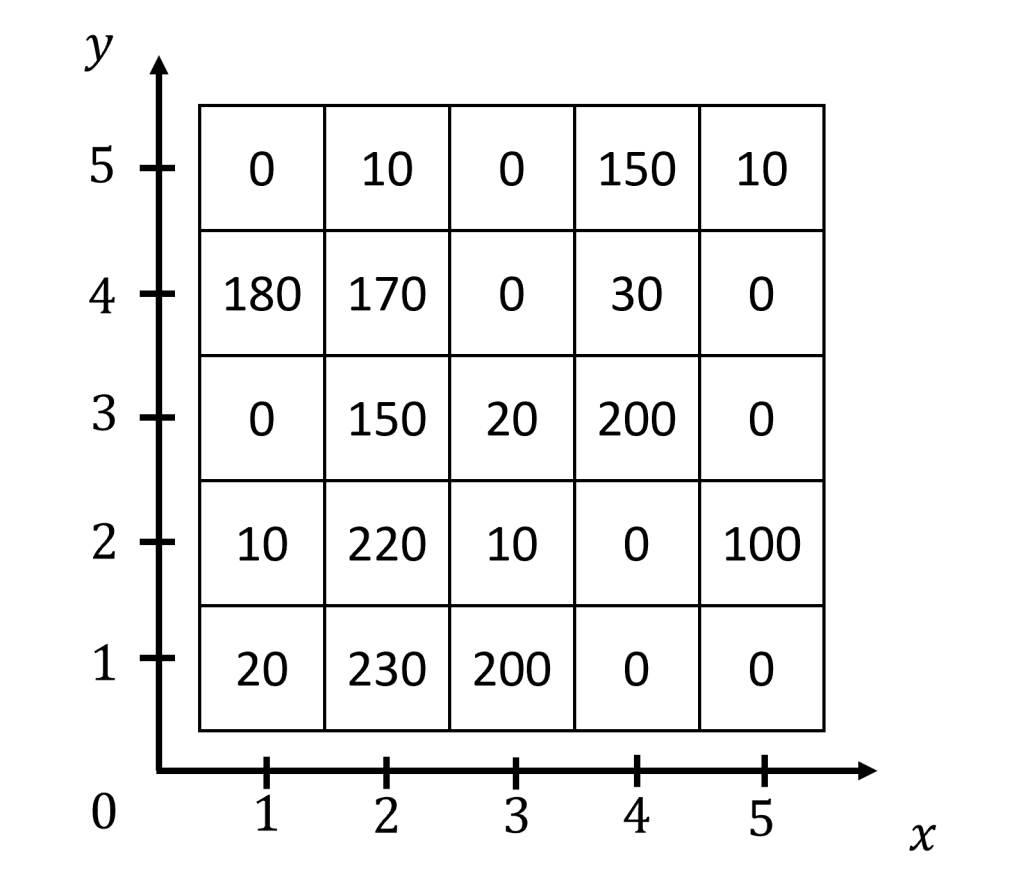
À présent que le cadre de travail est bien posé, nous pouvons commencer à définir ce qu’est un filtre gaussien et comment on l’utilise.

Filtre Gaussien :

Soit $\sigma > 0$ . Un filtre gaussien de paramètre $\sigma$ est une application

$G : (x, y) \mapsto G(x, y) = \sum\limits_{(x', y')} p_{(x, y)}(x', y') \times I(x', y')$

où $I(x', y')$ est l’intensité, c’est-à-dire le niveau de gris, au pixel de coordonnées $(x', y')$ . Et $p(x', y')$ correspond à la part de contribution du pixel $(x', y')$ dans la nouvelle intensité calculée pour le pixel $(x, y)$ .

$p(x', y')$ est calculé avec une gaussienne, d’où le nom de filtre gaussien. On a

$p_{(x, y)}(x', y') = A(x, y) \dfrac{1}{\sqrt{2 \pi} \sigma} e^{\dfrac{(x' - x)^2 + (y' - y)^2}{\sigma^2}}$

où $A(x, y)$ est un terme de normalisation qui est calculé de sorte que la somme des $p_{(x, y)}(x', y')$ vaut 1, à $(x, y)$ fixé.

Par les propriétés asymptotiques des fonctions gaussiennes, on considère que les pixels à une distance supérieure à $3 \sigma$ du pixel $(x, y)$ , auquel on applique le filtre, ne contribuent pas au calcul de $G(x, y)$ .

Après application d’un filtre gaussien de paramètre $\sigma = 1$ à l’image introduite précédemment, on obtient les valeurs numériques suivantes:

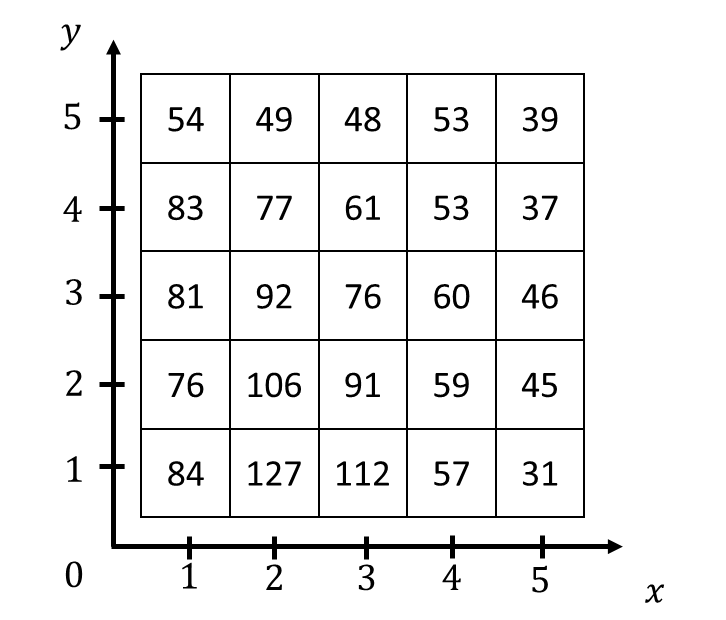
Valeurs numériques après application du filtre gaussien, de paramètre 1

Plus visuellement, voici la traduction en nuances de gris :

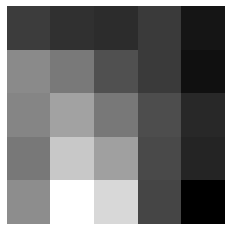
Image obtenue après application du filtre gaussien

Mettons à présent côte à côte les deux images :

On voit concrètement que l’image après application du filtre est plus lisse, mais aussi plus floue. Concrètement, appliquer le filtre gaussien revient à faire une moyenne pondérée des pixels, avec la particularité que les pixels contribuent d’autant plus qu’ils sont proches de l’endroit où l’on applique le filtre.

Exemple concret en Python

Voici ci-dessous un exemple d’application d’un filtre gaussien sur Python, que vous pouvez faire tourner directement chez vous.

	from skimage import data
	from skimage.color import rgb2gray

	# Chargement de l'image
	img = rgb2gray(data.chelsea())

	from scipy.ndimage import gaussian_filter

	# Application d'un filtre gaussien
	sigma = 5
	smooth_img = gaussian_filter(img, sigma)

	import matplotlib.pyplot as plt

	# Visualisation de l'effet du filtre
	fig, axes = plt.subplots(1, 2)
	images = [img, smooth_img]
	titles = ["Originale", "Filtre Gaussien"]
	for i, (image, title) in enumerate(zip(images, titles)):
	axes[i].imshow(image, cmap="gray")
	axes[i].axis("off")
	axes[i].set_title(title)
	plt.show()

view raw gaussian-filter.py hosted with ❤ by GitHub

Le code est divisé en trois parties:

Chargement de l’image à partir des données de skimage et conversion en niveaux de gris
Application d’un filtre gaussien
Visualisation des effets du filtre gaussien

gaussian_filter (scipy.ndimage)

Applique un filtre gaussien à l’image passée en argument.

Le résultat de ce code est l’image suivante:

On voit bien que l’image originale est rendue floue après application d’un filtre gaussien et que l’on a bien un lissage, car les teintes des poils du chat sont plus homogènes.

La Data Science

Filtre Gaussien

Introduction

Idée

Exemple concret en Python

Laisser un commentaire Annuler la réponse.

Filtre Gaussien

Introduction

Idée

Exemple concret en Python

Partager :

Laisser un commentaire Annuler la réponse.